Page 64 - 《中国药房》2022年4期

距离为5时，10批金母颗粒可聚为3类，其中S1、S3～S4 型预测能力参数（Q ）为0.723，即预测模型能力为72.3％，
2
聚为一类，S5～S6、S9聚为一类，S2、S7～S8、S10聚为一 提示该模型稳定、可靠 。采用相同方法绘制主成分分
[11]
类。结果见图4。 析得分图，详见图5。由图5可知，10批壮药金母颗粒可
25 20 分为 3 类，S1、S3～S4 为一类，位于得分图的左侧；S5～
20 9 13
mAU 15 11 S6、S9为一类，位于得分图的中部；S2、S7～S8、S10为一
10
5 2
0 类，位于得分图的右侧。这表明不同批次金母颗粒化学
0 20 40 60 80 100 120 140 成分的含量存在一定差异。
t/min
A.混合对照品溶液
25 3
20
mAU 15 11 2
10
5 2 9 13 20 1
0 S1 t[2] 0
0 20 40 60 80 100 120 140 －1
t/min －2
B.供试品溶液（编号S1）
－3
2.没食子酸；9.虎杖苷；11.芦丁；13.落新妇苷；20.山柰酚 －4
图2 没食子酸等成分的混合对照品溶液及供试品溶液 －15 －10 －5 0 5 10
t[1]
的HPLC图 图5 10批金母颗粒的主成分分析得分图
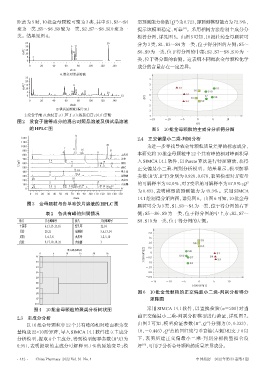
13
1 200 2.4 正交偏最小二乘-判别分析
1 100
20
1 000 为进一步寻找导致金母颗粒质量差异的标志成分，
7
900 11 16 21
6 15 17
800 土茯苓 本研究将10批金母颗粒中22个共有峰的相对峰面积导
700 3 4 8 苦参 入 SIMCA 14.1 软件，以 Pareto 算法进行特征缩放，获得
U/mV 600 9 18 19 22 黄柏
500 虎杖
12 14 正交偏最小二乘-判别分析模型。结果显示，模型解释
400 3 6 犁头草
2
2
300 13 14 金刚刺 参数（R X、R Y）分别为 0.920、0.678，表明模型对 X 变量
1 2 5 10
200 3 7 11 火炭母
100 2 13 17 大血藤 的可解释率为92.0％，对Y变量的可解释率为67.8％；Q 2
1 3 4 5 6 8 9 10 12 14 15 16 18 19 20 22
21
0 S1
为 0.493，表明模型的预测能力为 49.3％。采用 SIMCA
0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150
t/min 14.1绘制得分矩阵图，详见图6。由图6可知，10批金母
图3 金母颗粒与各单味饮片溶液的HPLC图
颗粒可分为3类，S1、S3～S4为一类，位于得分图的右下
表2 各共有峰的归属情况 侧；S5～S6、S9 为一类，位于得分图的中上方；S2、S7～
饮片 共有峰峰号 饮片 共有峰峰号 S8、S10为一类，位于得分图的左侧。
土茯苓 6、11、13、15、16 犁头草 12、14
苦参 20、21 金刚刺 3、6、13、14 2.0
黄柏 3、4、7、8 火炭母 1、2、5、10 1.5
虎杖 9、17、18、19、22 大血藤 3 1.0
平方欧氏距离 0.5
0 5 10 15 20 25 0
S1 1.060 86*t[2] －0.5
S4 －1.0
S3 －1.5
S5 －2.0
S9 －2.5
－15 －10 －5 0 5 10
S6
1.000 06*t[1]
S2
图 6 10 批金母颗粒的正交偏最小二乘-判别分析得分
S8
S7 矩阵图
S10
图4 10批金母颗粒的聚类分析树状图 采用 SIMCA 14.1 软件，以置换检验（n＝200）对当
2.3 主成分分析 前正交偏最小二乘-判别分析模型进行验证，详见图 7。
2
2
以10批金母颗粒中22个共有峰的相对峰面积为变 由图 7 可知，模型验证参数（R 、Q ）分别为（0，0.333）、
2
量构成22×10阶矩阵，导入SIMCA 14.1软件建立主成分 （0，－0.446），Q 点的回归线与垂直轴（左侧）相交于0以
分析模型，提取4个主成分，得到模型解释参数（R X）为 下，表明所建正交偏最小二乘-判别分析模型拟合良
2
[12]
0.951，表明提取的主成分可解释 95.1％的原始变量；模 好 ，可用于分析金母颗粒的质量差异成分。
·442 · China Pharmacy 2022 Vol. 33 No. 4 中国药房 2022年第33卷第4期