Page 16 - 中国药房2021年11期

0.08
0.025
0.020
0.06
概率密度 0.015 概率密度 0.04
0.010
0.02
0.005
0 0
0 20 40 60 80 －100 －50 0 50 100
Lev Tot
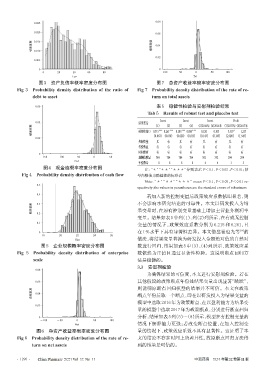
图3 资产负债率概率密度分布图 图7 总资产收益率概率密度分布图
Fig 3 Probability density distribution of the ratio of Fig 7 Probability density distribution of the rate of re-
debt to asset turn on total assets

0.06 表5 稳健性检验与安慰剂检验结果
Tab 5 Results of robust test and placebo test
Invest Invest Invest Profit
0.04 结果变量 （1） （2） （3） （4） （5）2016年（6）2016年 （7）2017年（8）2017年
概率密度 处理变量D 0.215 ＊＊＊ 0.261 ＊＊＊ 0.185 ＊＊＊ 0.085 ＊＊＊ 0.120 0.103 －3.519 ＊ －1.217
0.02 （0.063） （0.070） （0.020） （0.013） （0.143） （0.143） （2.020） （1.543）
控制变量 无 有 无 有 无 有 无 有
省份效应 有 有 有 有 有 有 有 有
时间效应 有 有 有 有 有 有 有 有
0
－150 －100 －50 0 50 观测值数量 784 784 784 784 392 392 294 294
Cof
年份数量 8 8 8 8 4 4 3 3
图4 现金流概率密度分布图 注：“＊”“＊＊”“＊＊＊”分别表示 P＜0.1、P＜0.05、P＜0.01；括
Fig 4 Probability density distribution of cash flow 号内数值为稳健性的标准误
Note：“＊”“＊＊”“＊＊＊”mean P＜0.1，P＜0.05，P＜0.01 re-
0.5
spectively；the values in parentheses are the standard errors of robustness
0.4
若加入新的控制变量后政策效应系数依旧显著，则
概率密度 0.3 不会影响本研究结论的可靠性。本文以研发投入为结
果变量时，在原有控制变量基础上增加主营业务利润率
0.2
变量。结果如表5中列（1）、列（2）列所示，在有或无控制
0.1
变量的情况下，政策效应系数分别为 0.215 和 0.261，且
[14]
0 在1％水平下具有显著性差异。本文借鉴崔也光等 的
18 20 22 24 26
Size 做法，将结果变量替换为研发投入金额绝对值的自然对
图5 企业规模概率密度分布图 数进行回归，结果如表5中（3）、（4）列所示，政策效应系
Fig 5 Probability density distribution of enterprise 数依然为正值且通过显著性检验。这说明断点回归方
scale 法是稳健的。
3.3 安慰剂检验
0.08
为确保结果的可信度，本文进行安慰剂检验。若在
0.06 其他假设的政策断点年份处结果变量出现显著“跳跃”，
概率密度 0.04 则说明原断点回归模型的结果并不可信。本文在政策
断点年份后取一个断点，即在以研发投入为结果变量的
模型中选取2016年为政策断点、在以盈利能力为结果变
0.02
量的模型中选取2017年为政策断点，分别进行断点回归
0 分析，结果如表5列（5）～（8）所示，模型在有控制变量的
－100 －50 0 50 100
Net 情况下解释能力更强；若改变断点位置，在加入控制变
图6 净资产收益率概率密度分布图 量的情况下，政策效应系数不具有显著性。这证明了本
Fig 6 Probability density distribution of the rate of re- 文的结论不存在时间上的差异性，故原断点回归方法得
turn on net assets 到的结果是可信的。

·1290 · China Pharmacy 2021 Vol. 32 No. 11 中国药房 2021年第32卷第11期