Page 109 - 《中国药房》2022年4期

分布拟合以获得临床试验随访期外的患者长期生存数 （willingness-to-pay，WTP）阈值比较以判断方案的经济
[10]
据 。本研究利用 GetData Graph Digitizer 2.26 软件从 性。根据世界卫生组织和《中国药物经济学评价指南
原始生存曲线中取点，利用R 4.0.5软件重构患者的个体 2020》的建议，本研究采用2020年我国1～3倍人均国内
生存数据并利用这些数据进行参数生存模型的拟合。 生产总值（gross domestic product，GDP）作为WTP阈值，
常见的参数分布形式包括指数分布、Weibull 分布、Gen- 即72 000～216 000元/QALY [14－16] 。

gamma 分布、Log-normal 分布、Log-logistic 分布和 Gom-
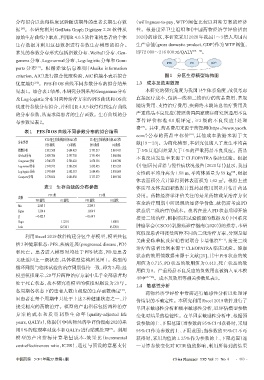
PFS PD 死亡
pertz 分布 。根据赤池信息准则（Akaike information
[11]
criterion，AIC）进行拟合优度检验，AIC值越小表示拟合 图1 分区生存模型结构图
[12]
优度越好 。PFS 和 OS 曲线不同参数分布的拟合结果 1.3 成本及效用数据
见表1。结合表1结果，本研究分别采用Gengamma分布 本研究的研究角度为我国卫生体系角度，故仅考虑
及Log-logistic分布对两种治疗方案的PFS曲线和OS曲 直接医疗成本，包括一线和二线治疗的药品费用、常规
线进行参数分布拟合，并利用R 4.0.5软件得到生存曲线 随访费用、支持治疗费用、疾病终末期姑息治疗费用及
的分布参数，从而求得患者的生存函数。生存曲线的分 严重药品不良反应（按照美国国家癌症研究所通用不良
布参数见表2。 事件评价标准 4.0 版评定，≥3 级的不良反应）处理
费 。其中，药品费用来源于药智网（https：//www.yaozh.
[17]
表1 PFS和OS曲线不同参数分布的拟合结果
[18]
com/）公布的药品中标价 ，其他成本数据来源于文
PTD组生存曲线拟合的AIC值 TD组生存曲线拟合的AIC值
分布类型 献[19－23]。为简化模型，本研究仅纳入了发生率均高
PFS曲线 OS曲线 PFS曲线 OS曲线
指数分布 2 812.508 2 604.423 2 793.217 2 867.413 于 5％且组间差异大于 1％的严重药品不良反应。药品
Weibull分布 2 809.786 2 597.758 2 791.424 2 860.806 不良反应发生率来源于 CLEOPATRA 临床试验。根据
Gengamma分布 2 746.275 2 586.622 2 674.336 2 849.740
Log-normal分布 2 747.915 2 586.558 2 692.455 2 855.235 《中国居民营养与慢性病状况报告（2020年）》显示，我国
Log-logistic分布 2 747.489 2 582.357 2 684.436 2 838.609 女性的平均身高为 1.58 m，平均体质量为 59 kg ，根据
[24]
Gompertz分布 2 770.856 2 606.030 2 737.277 2 869.382
体表面积公式计算得到体表面积为 1.62 m 。根据上述
2
表2 生存曲线的分布参数 体质量及体表面积数据计算药品使用剂量并估计药品
PTD组 TD组 费用。药物经济学评价关注的是某药物或某治疗方案
参数
PFS曲线 OS曲线 PFS曲线 OS曲线 在全治疗周期中所展现的经济学价值，故仍需考虑 PD
Mu 2.863 3 2.389 3
Sigma 1.254 6 1.056 9 状态后二线治疗的成本。患者在进入PD状态后即开始
Q －0.422 9 －0.614 9 接受二线治疗，根据临床试验披露的数据及《中国临床
Shape 1.521 0 1.600 0
Scale 62.518 1 43.270 0 肿瘤学会（CSCO）乳腺癌诊疗指南（2020）》的推荐，本研
究假设患者可接受两种不同的二线治疗方案，分别是恩
利用 Excel 2019 软件构建分区生存模型，模型共包
美曲妥珠单抗及拉帕替尼联合卡培他滨 [6－7] ，接受二线
括3种健康状态：PFS、疾病进展（progressed disease，PD）
治疗的患者比例来源于 CLEOPATRA 临床试验。健康
和死亡。患者进入模型时均处于 PFS 状态，PD 后患者
状态的效用值数据来源于文献[25]，其中 PFS 状态的效
无法返回上一级状态，具体模型结构图见图 1。模型的
用值为 0.715，PD 状态的效用值为 0.443，死亡状态的效
循环周期与临床试验的治疗周期保持一致，即为3周；经
用值为0。严重药品不良反应的负效用也被纳入至本模
模型模拟显示，20年后两种治疗方案中几乎全部患者均
型中 [25－26] 。成本及效用等相关参数见表3。
处于死亡状态，故本研究将模型的模拟时限设为20年。
1.4 敏感性分析
各周期各状态下的患者人数由相应的生存函数确定 ，
[13]
药物经济学评价中常需进行敏感性分析以处理评
且患者在每个周期中只处于上述3种健康状态之一，并 价结果的不确定性。本研究利用Excel 2019软件进行了
接受相应的药物治疗。模型的产出指标包括两种治疗 单因素敏感性分析和概率敏感性分析，以评估模型参数
方 案 的 成 本 和 质 量 调 整 生 命 年（quality-adjusted life 变化时结果的稳健性。在单因素敏感性分析中，根据预

years，QALYs），依据《中国药物经济学评价指南2020》采 设参数的上、下限范围（当参数的95％CI可获得时，采用
[14]
用5％的贴现率对成本和QALYs进行贴现处理 。利用 95％CI作为参数的上、下限范围；当参数的95％CI不可
模型的产出指标计算增量成本-效果比（incremental 获得时，采用均值的±25％作为参数的上、下限范围）逐
cost-effectiveness ratio，ICER），通过与预设的意愿支付 一计算参数变化对 ICER 值的影响，利用所得到的结果

中国药房 2022年第33卷第4期 China Pharmacy 2022 Vol. 33 No. 4 ·483 ·