Page 96 - 202008
P. 96
周 期 法 的 校 正 运 算 过 程 即 为 :9.90 + 1/2 - 0.32/2≈ 平滑的曲线的定积分,设Markov模型单位同期为n,k为
10.24年。 任一正整数,当 k 取 1,2…,T 时,tk=n,2n,…nT,即总周
1.0 期为nT。函数f(x)在区间[tk-1,tk+1]中的定积分则约等于
0.9 通过(tk-1,f(tk-1 ))、(tk,f(tk ))、(tk+1,f(tk+1 ))的曲线与x轴围
0.8
% 0.7 成的曲边梯形面积,函数 f(x)在区间[tk-1,tk+1]围成的面
患病人数比例, 0.5 积Ck为: tk+1-tk-1 [f(tk-1 )+4f(tk )+f(tk+1 )]
0.6
0.4
Ck=
0.3
0.2 6
0.1 则f(x)在[0,T]区间内的积分CT为:
0 T-1 2n T-1
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 CT= ∑ Ck= ∑ [f(tk-1 )+4f(tk )+f(tk+1 )]
循环周期,年 k=1,3,5… 6 k=1,3,5…
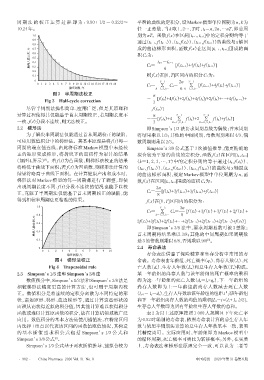
图3 半周期法校正 n
Fig 3 Half-cycle correction = 3 [f(t0 )+4f(t1 )+2f(t2 )+4f(t3 )f+2f(t4 )+…+4f(tnT -1 )+
尽管半周期法操作简单、应用广泛,但是其原理和 f (tnT )]
计算过程使得其仅能基于首末周期校正,若周期长度不 n [f(t0 )+4 ∑ f(tk )+2 ∑ f(tk )+f(tT )]
T-2
T-1
一致、f(t)分段不连续,则无法校正。 = 3 k=1,3,5… k=2,4,6…
2.2 梯形法 即Simpson’s 1/3 法要求周期总数为偶数;首末周期
为了解决半周期法仅能通过首末周期校正的缺陷, 将结果乘以1/3;其他的中间周期,奇数周期乘以4/3、偶
可应用数值积分中的梯形法。其基本原理是将f(t)每一 数周期则乘以2/3。
周期的端点值连线,由此将标准 Markov 模型中未经校 Simpson’s 3/8 公式基于 3 次插值推导,能更精确地
正的矩形变成梯形,将折线下的面积作为累计的结果 拟合较为平滑的曲线的定积分,函数 f(x)在区间[tk,tk+3]
[3]
(如图4所示) 。若f(t)为凸函数,则梯形法校正的结果 (k=1,2,3,…,T)中的定积分则约等于通过(tk,f(tk ))、
将略低于曲线下面积;若f(t)为凹函数,则梯形法计算的 (tk+1,f(tk+1 ))、(tk+2,f(tk+2 ))、(tk+3,f(tk+3 ))的曲线与x轴围成
结果将略高于曲线下面积。在计算健康产出和成本时, 的曲边梯形面积,规定 Markov 模型中单位周期为 n,函
梯形法对 Markov 模型的每一周期都进行了调整,即使 数f(x)在区间[tk,tk+3]围成的面积Ck为:
出现周期长度不同、f(t)分段不连续的情况也能予以校 3n
Ck= [f(tk )+3f(tk+1 )+3f(tk+2 )+f(tk+3 )]
正,克服了半周期法仅能基于首末周期校正的缺陷,能 8
得到相较半周期法更精准的结果。 f (x)在[0,T]区间内的积分为:
1.0 T-3 3n
CT= ∑ Ck= [f(t0 )+ 3f(t1 )+ 3f(t2 )+ 2f(t3 )+
0.8 k=1,3,5… 8
% 3f(t4 )+3f(t5 )+2f(t6 )+…+2f(tT-3 )+2f(tT-2 )+2f(tT-1 )+f(tT )]
患病人数比例, 0.6 即 Simpson’s 3/8 法中,要求周期总数可被 3 整除;
0.4
是3的倍数则乘以6/8,否则乘以9/8 。
[3]
0.2 首末周期将结果乘以 3/8;其他的中间周期如果周期数
0 2.4 寿命表法
0 1 2 3 4 5 6 7 8 9 10
循环周期,年 寿命表法借鉴了保险精算和生存分析中常用的寿
图4 梯形法校正 命表。寿命表由年龄组、死亡概率(qx )、尚存人数(lx )、死
Fig 4 Trapezoidal rule 亡人数(dx )、生存人年数(Lx )和总生存人年数(Tx )构成。
2.3 Simpson’s 1/3 法和Simpson’s 3/8法 某一年龄组的尚存人数与该年龄组的死亡概率的乘积
数值积分中,Simpson’s 1/3法和Simpson’s 3/8法是 即为这一年龄组的死亡人数(dx=lx×qx ),下一年龄组的
相较梯形法精度更高的计算方法,也可用于周期内校 尚存人数即为上一年龄组的尚存人数减去死亡人数
正。数值积分是将连续的定积分离散为不同特定的形 (lx+1= lx-dx ),生存人年数取该年龄组的组距t与该年龄组
状,诸如矩形、梯形、曲边梯形等,通过计算这些形状的 和下一年龄组尚存人数的均值的乘积[Lx=t×(lx+ lx+1 )/2],
面积从而获得近似的积分值,因其能计算难以获得积分 生存总人年数即为所有年龄组生存人年数的总和。
函数或难以计算原函数的积分,故在计算机领域被广泛 表 2 为以上述原理按照 1 000 人规模且下年死亡率
应用。数值积分的基本方法是使用插值法,在特定区间 为0.52时编制的寿命表,依照寿命表计算的总生存人年
内选择1组点以代表该区间的函数值取值情况,其构造 数与依照半周期法计算的总生存人年数基本一致,表明
的基本插 值 型 求 积 公 式 包 括 Simpson’s 1/3 公 式 和 其精度尚可。实际应用时,年龄组即为 Markov 模型中
Simpson’s 3/8公式 。 的循环周期,死亡概率可类比为转移概率;另外,在实质
[3]
Simpson’s 1/3公式基于两次插值推导,能拟合较为 上,寿命表法和梯形法原理完全一致,可以认为二者等
·982 · China Pharmacy 2020 Vol. 31 No. 8 中国药房 2020年第31卷第8期