Page 95 - 202008
P. 95
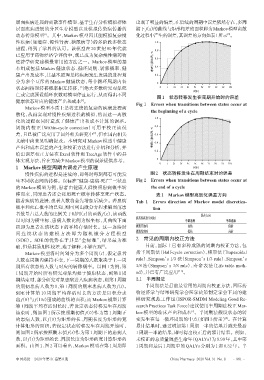
层面疾病进展的离散事件模型、基于生存分析模拟群体 出现了明显的偏差,在后续的周期中误差依然存在,多周
层面疾病进展的分区生存模型以及模拟传染病传播的 期下f(x)的曲线与矩形相差的面积即为Markov模型离散
[3]
[1]
动态传染模型 。其中,Markov模型因其能模拟复杂慢 化过程中产生的误差,其误差的方向如表1所示 。
性疾病(如癌症、慢性肾病、糖尿病等)的多阶段多状态 1.0
进程,得到了学界的认可。该模型在 20 世纪 80 年代就 0.8
%
已应用于药物经济学评价中,现已成为复杂慢性病药物 0.6
经济学研究建模最常用的方法之一。Markov 模型的基 患病人数比例,
本组成包括 Markov 健康状态、循环周期、转移概率、健 0.4
康产出及成本,其基本原理是将疾病发生发展的进程划 0.2
分为多个互斥的 Markov 健康状态,每个循环周期内各 0
状态间按照转移概率相互转移,当绝大多数研究对象死 0 t 2t 3t 4t 5t 6t 7t 8t 9t 10t
时间
亡或完成预设循环次数时模型停止运行,从而得出不同
图1 状态转移发生在周期开始时的误差
[1]
健康状态对应的健康产出和成本 。
Fig 1 Errors when transitions between states occur at
Markov 模型本质上是将连续的复杂的疾病进程离
the beginning of a cycle
散化,从而实现对慢性疾病进程的模拟,然而这一离散
1.0
化的过程也同时造成了健康产出和成本计算的误差。
周期内校正(Within-cycle correction)可用于校正该误 % 0.8
差,且已被广泛应用于国外相关研究中 ,但在国内相关 0.6
[2]
文献中尚未见明确提及。本研究对Markov模型中健康 患病人数比例, 0.4
产出和成本误差的产生和校正方法进行介绍和分析,并
0.2
给出误差校正方法在 Excel 软件和 TreeAge 软件中的具
体实现方法,旨在为减少Markov模型的误差提供参考。 0
0 t 2t 3t 4t 5t 6t 7t 8t 9t 10t
1 Markov模型周期内误差产生原理 时间
慢性疾病的进程是连续的,即每时每刻都有可能发 图2 状态转移发生在周期结束时的误差
生不同状态间的转移。以标准“健康-患病-死亡”三状态 Fig 2 Errors when transitions between states occur at
的 Markov 模型为例,患者由健康人群按照患病概率转 the end of a cycle
移而来,同时患者还会按照死亡概率转移至死亡状态。 表1 Markov模型离散化误差方向
随着疾病的进展,患者人数将会先增加后减少。若患病 Tab 1 Errors direction of Markov model discretiza-
概率和死亡概率均已知,则可列出微分方程求解当前患 tion
者数量占总人数的比例关于时间(x)的函数f(x),该函数 误差方向
状态转移发生时间
以时间为横坐标、患病人数比例为纵坐标,其曲线下面 单调递增 单调递减
积即为患者在该状态下的平均存活时长。这一连续时 周期开始时 高估 低估
周期结束时 低估 高估
间 连 续 状 态 的 建 模 方 法 即 为 随 机 微 分 方 程 模 型
(SDE)。SDE 的优势在于其是“金标准”,结果最为准 2 常见的周期内校正方法
确,但是其易用性较差,难于解释,不够直观 。 目前,国际上已有多种成熟的周期内校正方法,包
[3]
Markov 模型将时间划分为多个周期(t),假定患者 括半周期法(Half-cycle correction)、梯形法(Trapezoidal
人数在周期内保持不变,下一周期的人数取决于上一周 rule)、Simpson’s 1/3 法(Simpson’s 1/3 rule)、Simpson’s
期所有状态的人数与对应的转移概率。以图1为例,第 3/8 法(Simpson’s 3/8 rule)、寿命表法(Life table meth-
1 周期开始时所有研究对象均处于健康状态,到第 1 周 od),并已有广泛应用 [4-6] 。
期结束时,部分研究对象患病进入疾病状态,则第1周期 2.1 半周期法
的期初患病人数为 0,第 1 周期的期末患病人数为 f(t)。 半周期法是目前最常用的周期内校正方法,国际药
SDE 计算第 10 周期平均存活时长的方法是以积分求 物经济学与结果研究学会医学决策制定学会下属的建
出 f(0)与f(10t)围成的曲线的面积;而Markov模型计算 模研究规范工作组(ISPOR-SMDM Modeling Good Re-
第1周期平均存活时长时,若设定状态转移发生在周期 search Practices Task Force)建议使用半周期法校正Mar-
[7]
结束时,则如图 1 所示按照期初值 f(0)作为第 1 周期下 kov 模型的临床产出和成本 。半周期法假设状态的转
[8]
的患病人数,以 f(0)为矩形的长、周期长度为矩形的宽 变发生在每一循环周期的中点(如图3所示) 。在计算
计算矩形的面积;若设定状态转移发生在周期开始时, 累计结果时,通过增加第1周期一半的结果并减去最后
则如图 2 所示按照期末值 f(t)作为第 1 周期下的患病人 1周期一半的结果,即可得出校正后的累计结果。例如,
数,以f(t)为矩形的长、周期长度为矩形的宽计算矩形的 未校正的总质量调整生命年(QALYs)为9.90年,其中第
面积。由图1、图2可以看出,Markov模型在第1周期即 1周期和最后1周期中的QALYs分别为1和0.32年。半
中国药房 2020年第31卷第8期 China Pharmacy 2020 Vol. 31 No. 8 ·981 ·