Page 111 - 《中国药房》2022年7期
P. 111
然比检验无法使用;而贝叶斯信息准则(Bayesian infor- 效用积分体系下,EQ-5D-5L所能获得的最小值,而“ulim
mation criterion,BIC)则是一个非常适合的方式,可以很 (1)”为最大值。此处采用从中国类风湿性关节炎患者
好地指示出分布类型合适的数量,以及不同分布类型似 人群的EQ-5D-5L效用积分体系获得的最小值(-0.391)
然值的图形。分布类型数量的增加,会使模型拟合度有 和最大值(1)。需要注意的是,若此处不进行设定,模型
一定增加,但在一定程度上也会使这个分布类型本身失 默认使用英国的效用积分体系。“aldvmm”的命令可通过
去意义(例如将某几个值作为一个分布类型单独列出, 在Stata 16软件中输入“findit aldvmm”获取(下载并安装
而实际这些值为异常值,并不能很好地代表实际分布情 “SJ-16-4 st0401_1”)。ALDVMM 的命令语法以及选项
[12]
况)。而如果在分布类型数量与单个分布的大小(分布 等详情可参考 Hernández Alava 等 发表于 2015 年的文
涉及的范围)之间做出一个折中选择,则可以使这个模 献,该文献对相关问题进行了较为详细的描述。
型更具有意义,从而做到对样本外数据进行更有效的预 表1 模型演示结果
[11]
测 。 Number of obs=169
对于模型拟合度的检验,由于ALDVMM存在嵌套, Log likelihood=45.751 958 Wald chi2(3)=234.37
Prob>chi2=0.000 0
2
Hernández Alava 等 并没有使用传统的调整后 R 、平均 eq5d5l Coef. Std. Err. z P>z 95%CI
[11]
误差(mean error,ME)、平均绝对误差(mean absolute haqdi -0.325 330 0.025 196 -12.91 0 -0.374 710~-0.275 940
error,MAE)以 及 均 方 根 误 差(root mean square error, age -0.002 360 0.001 222 -1.93 0.053 -0.004 760~0.000 035
gender -0.172 500 0.029 656 -5.82 0 -0.230 630~-0.114 380
RMSE),而是使用了赤池信息准则(Akaike information _cons 1.308 816 0.069 171 18.92 0 1.173 243~1.444 389
criteria,AIC)和BIC。 /lns_1 -1.701 750 0.054 739 -31.09 0 -1.809 040~-1.594 470
sigma1 0.182 364 0.009 982 0.163 811~0.203 017
1.4 模型演示示例
Log likelihood:对数似然值;Number of obs:样本量;Wald chi2
为了让读者更好地了解 ALDVMM,本文使用笔者
(3):Wald χ 检验;Prob>chi2:P值
2
所在团队正进行的一项研究数据进行简单示例,通过
2 模型优势
ALVDMM 模型将 HAQ-DI 映射到 EQ-5D-5L 上。该项
从已有的研究结果来看,ALDVMM 相对于传统映
数据包含了中国类风湿性关节炎患者的 EQ-5D-5L 得
射模型具有明显的优势,主要体现在以下几个方面:
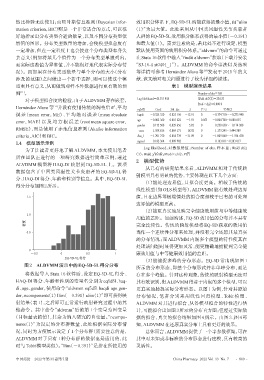
分、HAQ-DI得分、年龄和性别等信息。其中,EQ-5D-5L
(1)能处理边界值,且拟合度更高。相较于传统的
得分分布如图2所示。
线性模型(如 OLS 模型等),ALDVMM 能有效处理边界
1.5 值,且在边界等极端值处的拟合度相较于已有的可处理
边界值的模型更高。
(2)能更真实地反映完全健康效用值与中等健康效
1.0
用值的差距。如前所述,EQ-5D效用值的分布并不具有
密度 完全连续性。传统的映射模型将 EQ-5D 获取的效用值
0.5 当作一个连续性分布来处理,并没有完全还原其最真实
的分布情况;而 ALDVMM 内嵌多个模型的特性使其在
处理该问题时显得更加灵活,能更精确地捕捉到完全健
0
-0.5 0 0.5 1 康效用值与中等健康效用值的差距。
EQ-5D-5L得分
(3)能捕捉多峰的分布形态。EQ-5D 常出现如图 1
图2 ALDVMM演示中的EQ-5D-5L得分分布
所示的分布形态,即整个分布形式并非单峰分布,而是
将数据导入 Stata 16 软件后,设定 EQ-5D-5L 得分、 存在多个峰值。针对这种现象,传统的映射模型无法对
HAQ-DI 得分、年龄和性别的变量名分别为 eq5d5l、haq- 其有效识别,但ALDVMM得益于内嵌的多个模型,可以
di、age、gender,使用命令“aldvmm eq5d5l haqdi age gen- 更真实地捕捉实际分布形态。以图1为例,针对其原始
der,ncomponents(1)llim(-0.391)ulim(1)”即可获得映 分布情况,笔者分别采用线性回归模型、Tobit 模型、
射结果(表 1),之后即可正常运行映射研究过程中的其 ALDVMM 对其进行拟合,从各模型拟合的特性进行估
他命令。其中命令“aldvmm”后的第 1 个变量为因变量 计,可能拟合出如图3所示的分布直方图;但经过实际数
(目标量表的值),其余为纳入研究的自变量。“ncompo- 据的拟合,真实的拟合结果如图 4 所示。由图 3、图 4 可
nents(1)”为设定的分布群数量,此处根据实际分布情 知,ALDVMM在还原真实分布上具有更好的效果。
况,同时为方便展示设定了1个分布群(需要注意的是, 总体而言,ALDVMM提供了一个半参数框架,可在
ALDVMM 对于只有 1 种分布群的数据也是适用的,此 其中对未知或非标准的分布形态进行建模,具有较高的
时与 Tobit 模型类似)。“llim(-0.391)”是指在所使用的 灵活性。
中国药房 2022年第33卷第7期 China Pharmacy 2022 Vol. 33 No. 7 ·869 ·