Page 99 - 2021年14期

[12]
据估计，2018年全球有1 700万癌症新发病例和950 存曲线直接估计每个健康状态下的人数比例 。如果N
万死亡病例，到2040年，这一人数预估会增长到2 750万 代表模型中的健康状态数，假设第n个健康状态的累积
[1]
和1 630万 。随着临床诊治水平的提升，涌现出了较多 生存概率为S（t）n（n＝1，2，…，N）（累积生存概率表示观
的新型抗肿瘤治疗方案，在延长患者生存期和提高患者 察对象生存时间大于t时刻的概率），那么第1个健康状
生存质量方面获益显著，然而，这些新型治疗方案的治 态的人数比例将直接由 S（t）1 决定，第 2 个直到第（N－
[2]
疗成本通常十分高昂 。随着我国医保支出的持续增 1）个状态的人数比例分别由S（t）n－[S（t）n－1]（n＞1且
长，评估新方案多花的成本是否因改善健康产出而具有 n≤N－1）决定；而最后一个状态（一般为死亡）的人数比
经济性成为用药决策中一项较为重要的问题。 例由1－[S（t）n－1]（n＝N）决定。因此，若假设模型中有
[13]
通常，抗肿瘤药物治疗方案的药物经济学评估均采 N个健康状态，模型构建则需要（N－1）条生存曲线 。
用决策分析模型，该模型可为综合现有证据提供定量框 PartSA模型最常采用无进展（progression free，PF）、
架，并生成相关的成本-效果评估结果，进而为相关决策 疾病进展（progression disease，PD）、死亡（death）等 3 种
提供证据支持 [3－5] 。决策分析常用的模型包括决策树模 健康状态来构建模型，这种情况下通常需要两条生存曲
型、马尔可夫（Markov）模型（离散或连续）、分区生存 线：总体生存（overall survival，OS）曲线和无进展生存
（PartSA）模型和个体样本模型等。由于不同模型的构 （progression free survival，PFS）曲线。其中，PFS 曲线下
建技术与特征差异较大，因此选择不同的建模方法会对 方的区域代表尚未进展的患者比例，OS 和 PFS 曲线之
所模拟的结果产生较大影响 [6－7] ，但限于资料难以获得 间的区域代表已进展且仍存活的患者比例，其余区域代
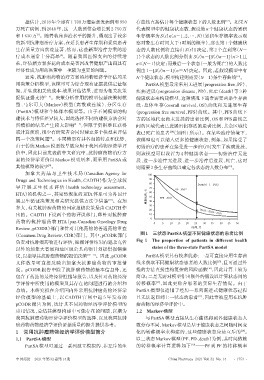
或计算烦琐，很少有研究者会同时建立多个模型来评估 表已死亡的患者 （如图 1 所示）。在某些治疗情境下，
[14]
[8]
同一个决策问题 。不同模型有其各自的特点和优势， 该模型也可以纳入更多的健康状态，例如，如果接受了
由于传统Markov模型较早被应用于我国药物经济学评 初始治疗的患者在接受进一步治疗时发生了疾病进展，
价中，因此目前发表的中文研究中，抗肿瘤药物治疗方 则该模型可以设置为 4 种健康状态——初始治疗无进
案的经济学评价以 Markov 模型居多，而采用 PartSA 或 展、进一步治疗无进展、进一步治疗后进展、死亡，这时
[9]
其他模型的较少 。 则需要3条生存曲线以确定各状态的人数分布 。
[13]
加拿大药品与卫生技术局（Canadian Agency for 100
Drugs and Technologies in Health，CADTH）作为全球较 90
80 Death（t）＝1－S（t）2
早 开 展 卫 生 技 术 评 估（health technology assessment， 70
％ 60 OS＝S（t）2
HTA）的机构之一，其完整规范的 HTA 体系可为各国开 50
[10]
展卫生循证决策及相关研究提供方法学借鉴 。在加 患者比例， 40 PFS＝S（t）1
拿大，有关抗肿瘤药物的国家报销决策是由 CADTH 作 30
20
出的。CADTH 下设两个药物评议部门，即针对抗肿瘤 10 PD （ t ） ＝S （ t ） 2－S （ t ） 1
0
药物的抗肿瘤药物 HTA（pan-Canadian Oncology Drug
0 5 10 15 20 25 30 35 40 45 50
Review，pCODR）部门和针对其他药物的普通药物审查 时间，月
（Common Drug Review，CDR）部门。其中，pCODR部门 图1 三状态PartSA模型不同健康状态的患者比例
负责对抗肿瘤药物进行评估，根据评估结果向魁北克省 Fig 1 The proportion of patients in different health
states of the three-state PartSA model
以外的加拿大省级和地区级公共药物计划提供报销建
议，以指导其抗肿瘤药物的报销决策 [10－11] 。因此，pCODR PartSA模型具有较多优势：一是可直接应用生存曲
[15]
文件数量可直接反映出加拿大抗肿瘤药物的审批情 线来获取不同健康状态患者的人数比例 ，且可通过外
[16]
况。pCODR 报告中除了抗肿瘤药物的基本信息外，还 推的方法直接重构复杂的风险函数 ，因此计算上较为
包含了药品的最终经济性指导报告，以及针对药物经济 简单；二是无需对模型作出额外的假设以计算状态间的
[17]
学评价中所使用的模型及其存在的问题进行的介绍和 转移概率 ，因此更贴合患者的实际生存情况。由于
总结。本研究拟在介绍国内外常用抗肿瘤药物经济学 PartSA 模型仅适用于经历一系列渐进式健康状态过程
[17]
评价模型的基础上，以 CADTH 官网中近 5 年发布的 且无法返回到上一状态的患者 ，因此常被应用在抗肿
pCODR 报告为例，统计其不同药物经济学评价模型的 瘤药物的经济学评价中。
应用情况，总结其模型构建中可能存在的问题，以期为 1.2 Markov模型
我国抗肿瘤药物经济学评价模型的选择、以及我国抗肿 与 PartSA 模型直接从生存曲线得到各健康状态人
瘤药物药物经济学评价证据质量的提升提供参考。 数分布不同，Markov模型是基于健康状态之间随时间变
1 常用抗肿瘤药物经济学评价模型简介 化的转移概率来构建的，这些健康状态应是互斥的 。
[18]
1.1 PartSA模型 以三状态Markov模型（PF、PD、death）为例，其时间依赖
[19]
PartSA模型可通过一系列独立模拟的、非互斥的生 的转移概率计算逻辑如下 ——PF 到 PF 的转移概率

中国药房 2021年第32卷第14期 China Pharmacy 2021 Vol. 32 No. 14 ·1753 ·